The Inclusion Problem

Group X consists of 100 children who have their own teacher, who go to the library instead of gym, who are late to school every morning, who wear the same hat every day, who get to ride in the elevator, who never notice their name being called, who draw the same field of flowers with markers in art, who leave early for lunch every day, who whisper into their hands, who pace and clap before leaving a room, who sometimes fall asleep in the sun at recess and miss the start of music class, who love to spin in their chairs, spin and spin and never get dizzy.

Group Y consists of 100 children who have brown eyes and are right-handed.

If a boy from Group X is placed in a new class, if he arrives with his name sewn onto a blue canvas bag, if he gets to play games on a laptop during silent reading time, if he leaves with a tall woman every Wednesday during math, if he wears special headphones that come in a rechargeable case, if he rocks and sucks his sleeve when he listens to music, if he hits himself in the head when he loses a game, when his headphones have not been recharged, when the wi-fi is down, when his words will not come, how long will it take for the other children to ask questions?

The Food Web Problem

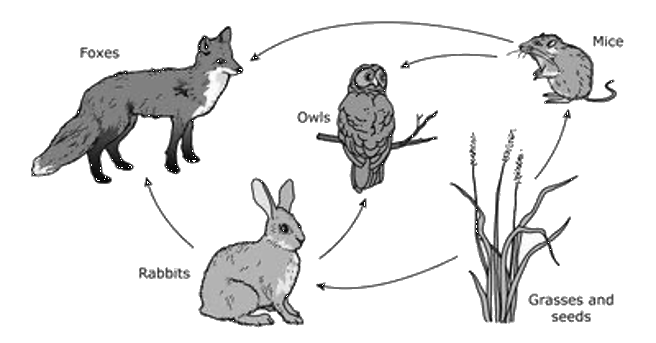
A food web is a system that absorbs a creature’s death. A meadow can be a system if you recall the rain a claw collects, the wind and where it blooms, a single seed obscured by fur. If a rabbit misses when the silhouette of an owl avoids the moon, where does the energy in grasses go? Make a graph that shows how non-essential animals are ignored. Place an x beside the blooming spiral, then shade the section that reflects a fox’s click.

The Logic Problem

In a digital forest, owls are always floral. Floral owls never float. Mirrored owls float. Forests float. Pixels bloom. Pixels are always mirrored. Owls never bloom. Owls always mirror forests. Digital pixels are never floral. Floral pixels float. Some forests bloom floral mirrors.

Assume all of this is true.

How often do owls bloom pixels?
Would a mirrored forest bloom digital owls?

The Night Problem

Two girls are gathering shapes from the word shadow. They understand that any language needs a garden, so they scatter circles in perfect tandem. They make a kaleidoscope with seeds. When they aim it at the moon, they find a constellation that has never been named. One girl sees a hanging plant. The other, a handful of knives. Explain the girls’ results, then sketch the sky they share.

The Plotting Problem

A boy folds a map into a crooked cylinder then looks around for help. He’s trying to find the area of a wilderness of wanting. He’s been asked to graph a lake’s desire to ferry a swan. He checks the clock again and wonders how to figure out why a storm returns a bell’s recursive lull. Where should he begin? Which formula or rule could possibly apply to his bright, percussive panic?

The Symbiosis Problem

A tree rejects a paper hive. It drips from a branch like an axe wrapped in wool, as a graft of bark weaves itself into place. The evicted colony finds a lake of milk to infect. Unopened flowers rot on its shore. Graph the curve of a queen reclined, then predict the circumference of her first seven eggs. If each wax chalice remains intact, how many times can collapse be deferred?

Matthew Mahaney is a poetry fellow in the PhD program at the University of Louisiana at Lafayette. His most recent book is The Plural Space (Salò Press, 2016). In games of Truth or Dare, he will always pick Truth but might still lie.